spherical_harmonic#

The spherical_harmonic module provides functions for evaluation of the real, 2D, orthonormal, spherical harmonics and their first two derivatives. A single spherical harmonic is a function in 2D spherical space with a degree and order, \(n\) and \(m\),

\[Y_n^m (\theta, \phi) ,\]

where \(\theta\) is the colatitude in \([0,\pi]\) and \(\phi\) is the longitude in \([0,2\pi]\). Each harmonic is the product of an associated Legendre polynomial in the colatitude coordinate and a sine or cosine in the longitude coordinate. Whether the associated Legendre function is accompanied by a sine or a cosine is (for the real harmonics) determined by the sign of the order (\(m\)). In full, the harmonics are implemented here as

\begin{equation} Y_n^m(\theta,\phi) = \begin{cases} \sqrt{2} \sin(|m|\phi) P_n^{|m|}(\cos\theta) & m < 0 \\ P_n^{m}(\cos\theta) & m = 0 \\ \sqrt{2} \cos(m\phi) P_n^{m}(\cos\theta) & m > 0 \end{cases} \end{equation}

where \(P_n^m\) is an associated Legendre polynomial. The harmonics here are orthonormal.

This module contains functions for evaluating the spherical harmonics, their gradients, and their laplacians. It doesn’t contain functions to perform transforms from values on the sphere to spherical harmonic expansion coefficients. The module also contains some functions for generating grids in spherical space and for generating random spherical harmonic expansions with specific power density properties (noise). The Expansion class stores harmonic coefficients, evaluates them, and may be multiplied/divided by scalars. For evaluating only a few expansions at a few sets of points, using the sph_har function or Expansion class should be fine. For evaluating many expansions (of the same size) at the same set of points, consider using the sph_har_matrix function.

orthopoly.spherical_harmonic.cart2sph(x, y, z)#

Converts 3D cartesian coordinates into spherical coordinates

Parameters:

x (array) – x coordinates
y (array) – y coordinates
z (array) – z coordinates

Returns:

tuple containing

spherical radii
polar angles in \([0,\pi]\)
azimuthal angles in \([0,2\pi]\)

orthopoly.spherical_harmonic.sph2cart(r, theta, phi)#

Converts spherical coordinates into 3D cartesian coordinates

Parameters:

r (array) – spherical radii
theta (array) – polar angles in \([0,\pi]\)
phi (array) – azimuthal angles in \([0,2\pi]\)

Returns:

tuple containing

x coordinates
y coordinates
z coordinates

orthopoly.spherical_harmonic.latlon2sph(lat, lon)#

Converts from latitude and longitude in degrees to radians

Parameters:

lat (array) – latitude in [-90,90]
lon (array) – longitude in [-180,180]

Returns:

tuple containing

array of polar angles in \([0,\pi]\)
array of azimuthal angles in \([0,2\pi]\)

orthopoly.spherical_harmonic.sph2latlon(theta, phi)#

Converts from radians to latitude and longitude

Parameters:

theta (array) – polar angle in \([0,\pi]\)
phi (array) – azimuthal angle in \([0,2\pi]\)

Returns:

tuple containing

array of latitudes in [-90,90]
array of longitudes in [-180,180]

orthopoly.spherical_harmonic.T2nharm(N)#: Computes the number of functions/harmonics in a triangular truncation of degree N

orthopoly.spherical_harmonic.R2nharm(N, M)#: Computes the number of functions/harmonics in a rhomboidal truncation of degree N, order width M

orthopoly.spherical_harmonic.Tnm(N)#

Gets arrays representing the degrees and orders of a trianglular truncation of maximum degree N

Parameters:

N (int) – degree of truncation

Returns:

tuple containing

the degrees of the functions in the expansion
the orders of the functions in the expansion

orthopoly.spherical_harmonic.Rnm(N, M)#

Gets arrays representing the degrees and orders of a rhomboidal truncation of maximum degree N and order width M

Parameters:

N (int) – highest degree in truncation
M (int) – highest number of orders in each degree

Returns:

tuple containing

the degrees of the functions in the expansion
the orders of the functions in the expansion

orthopoly.spherical_harmonic.sph_har_norm(n, m)#

Evaluates, with an iteration instead of direct factorials to help avoid overflow, the normalization factor for the spherical harmonics,

\begin{equation} \sqrt{ \frac{ (2 - \delta_{m,0})(2n + 1)(n - m)! }{ 4 \pi (n + m)! } } \, , \end{equation}

where \(\delta\) is the kronecker delta.

This can be used to unorthonormalize the spherical harmonics given by sph_har or to orthonormalize some unorthonormalized functions. The factorials are evaluated to avoid underflow, but very high orders may still be problematic. Because the orthonormalization is built into the Legendre polynomials used to construct the harmonics in this module, this function is not called to evaluate the harmonics or the legendre polynomials. It’s just a convenience function for converting between orthonormalized and unorthonormalized harmonics.

Parameters:

n (int) – degree of harmonic
m (int) – order of harmonic

Returns:

orthonormalization factor

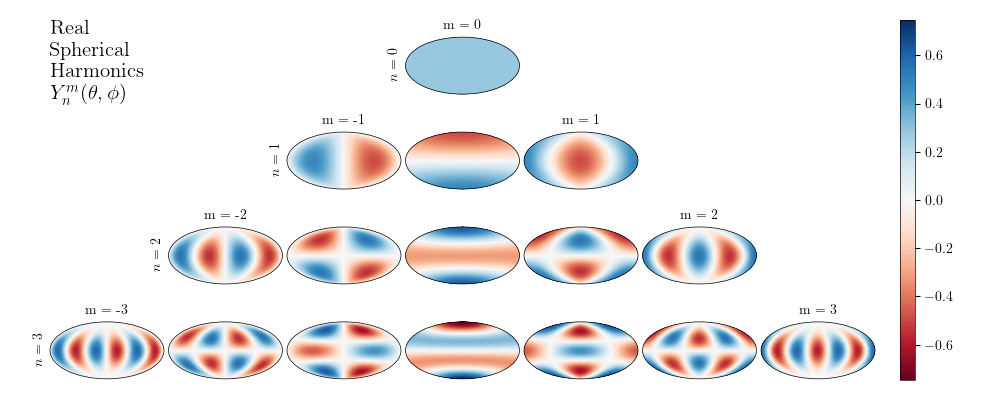
orthopoly.spherical_harmonic.sph_har(t, p, n, m)#

Evaluate the real, orthonormal, spherical harmonic of degree n and order m.

These are associated Legendre polynomials (legen_hat) in latitude (\(\theta\)) and sine/cosine in longitude (\(\phi\)).

where \(P_n^m\) is the normalized associated Legendre function implemented in this module as legen_hat or legen_theta. The normalization ensures that the functions are orthonormal. More info can be found in the references below, among many other places

Press, William H., et al. Numerical recipes 3rd edition: The art of scientific computing. Cambridge university press, 2007.
Dahlen, F.A. and, and Jeroen Tromp. Theoretical global seismology. Princeton university press, 1998.
Fornberg, Bengt. A Practical Guide to Pseudospectral Methods. Cambridge University Press, 1996.

Parameters:

t (array/float) – \(\theta\), colatitude coordinate in \([0,\pi]\) (can be an array)
p (array/float) – \(\phi\), azimuth/longitude coordinate in \([0,2\pi]\) (can be an array)
n (int) – degree of harmonic
m (int) – order of harmonic

Returns:

\(Y_n^m(\phi,\theta)\)

orthopoly.spherical_harmonic.sph_har_sum(t, p, a, yn, ym)#

Evaluates a spherical harmonic expansion at arbitrary points with arbitrary orders and degrees

Parameters:

t (array/float) – \(\theta\), colatitude coordinate in \([0,\pi]\) (can be an array)
p (array/float) – \(\phi\), azimuth/longitude coordinate in \([0,2\pi]\) (can be an array)
a (array) – spherical harmonic expansion coefficients
yn (iterable) – the degrees of the functions in the expansion
ym (iterable) – the orders of the functions in the expansion

Returns:

value of expansion at \(\sum_{i} a_i Y_{n_i}^{m_i}(\phi,\theta)\)

orthopoly.spherical_harmonic.grad_sph_har(t, p, n, m, R=1)#

Evaluates the gradient of the real, orthonormal, spherical harmonics defined in sph_har

Parameters:

t (array/float) – \(\theta\), colatitude coordinate in \([0,\pi]\) (can be an array)
p (array/float) – \(\phi\), azimuth/longitude coordinate in \([0,2\pi]\) (can be an array)
n (int) – degree of harmonic
m (int) – order of harmonic
R (float) – the radius of the spherical surface, which scales the derivatives

Returns:

tuple containing

gradient component in the \(\theta\) direction
gradient component in the \(\phi\) direction

orthopoly.spherical_harmonic.lap_sph_har(t, p, n, m, R=1)#

Evaluates the Laplacian of the real, orthonormal, spherical harmonics defined in sph_har

Parameters:

t (array/float) – \(\theta\), colatitude coordinate in \([0,\pi]\) (can be an array)
p (array/float) – \(\phi\), azimuth/longitude coordinate in \([0,2\pi]\) (can be an array)
n (int) – degree of harmonic
m (int) – order of harmonic
R (float) – the radius of the spherical surface, which scales the derivatives

Returns:

\(\nabla^2 Y_n^m(\theta,\phi)\)

orthopoly.spherical_harmonic.sph_har_matrix(t, p, yn, ym)#

Assembles the matrix of spherical harmonic function values for an arbitrary subset of harmonics using the latitude coordinates t and the longitude coordinates p

Parameters:

t (array/float) – \(\theta\), colatitude coordinate in \([0,\pi]\) (can be an array)
p (array/float) – \(\phi\), azimuth/longitude coordinate in \([0,2\pi]\) (can be an array)
yn (array) – the degrees of the functions in the expansion
ym (array) – the orders of the functions in the expansion

Returns:

matrix with shape (npts,nharm) containing the values of the harmonics at the input points (each row for a point, each column for a harmonic). This matrix is multiplied directly with expansion coefficients to evaluate the expansion at the given points. That is, the returned matrix \(Y\) sasatisfies \(Y a = f\), where a is a vector of nharm expansion coefficients and f is a vector of npts sampled points over the sphere.

orthopoly.spherical_harmonic.sph_har_T_matrix(t, p, N)#

Assembles the matrix of spherical harmonic function values for a triangular truncation of degree N using the latitude coordinates t and the longitude coordinates p

Parameters:

t (array/float) – \(\theta\), colatitude coordinate in \([0,\pi]\) (can be an array)
p (array/float) – \(\phi\), azimuth/longitude coordinate in \([0,2\pi]\) (can be an array)
N (int) – degree of triangular truncation

Returns:

tuple containing

matrix with shape (npts,nharm) containing the values of the harmonics at the input points (each row for a point, each column for a harmonic). This matrix is multiplied directly with expansion coefficients to evaluate the expansion at the given points. That is, the returned matrix \(Y\) sasatisfies \(Y a = f\), where a is a vector of nharm expansion coefficients and f is a vector of npts sampled points over the sphere.
array of the degrees of the functions in the expansion
array of the orders of the functions in the expansion

orthopoly.spherical_harmonic.sph_har_R_matrix(t, p, N, M)#

Assembles the matrix of spherical harmonic function values for a rhomboidal truncation of degree N and order width M, using the latitude coordinates t and the longitude coordinates p

Parameters:

t (array/float) – \(\theta\), colatitude coordinate in \([0,\pi]\) (can be an array)
p (array/float) – \(\phi\), azimuth/longitude coordinate in \([0,2\pi]\) (can be an array)
N (int) – degree of rhomboidal truncation
M (int) – order width of rhomboidal truncation

returns: tuple containing

matrix with shape (npts,nharm) containing the values of the harmonics at the input points (each row for a point, each column for a harmonic). This matrix is multiplied directly with expansion coefficients to evaluate the expansion at the given points. That is, the returned matrix \(Y\) sasatisfies \(Y a = f\), where a is a vector of nharm expansion coefficients and f is a vector of npts sampled points over the sphere.

array of the degrees of the functions in the expansion

array of the orders of the functions in the expansion

orthopoly.spherical_harmonic.grid_regular(nth, nph=None, poles=True)#

Creates a grid of points regularly spaced in each direction. It can include points right at the poles or can be a nice 2D array by starting and stopping off the boundaries

Parameters:

nth (int) – number of theta points
nph (int) – number of phi points (will be 2*nth if unused)
poles (bool) – include two points exactly at the poles or not

Returns:

tuple containing

\(\theta\), array of colatitude coordinates in \([0,\pi]\)
\(\phi\), array of azimuth/longitude coordinates in \([0,2\pi]\)

orthopoly.spherical_harmonic.grid_fibonacci(n)#

Arranges \(n\) or \(n+1\) points (must be an odd number) in a Fibonacci lattice/grid over the surface of a sphere. The grid achieves nearly uniform spacing over the sphere and is remarkably easy to calculate, making it an attractive option. For details and explanation, see

Gonzalez, Alvaro. “Measurement of areas on a sphere using Fibonacci and latitude-longitude lattices.” Mathematical Geosciences 42.1 (2010): 49.

Parameters:

n (int) – desired number of points (output might have one extra point)

Returns:

tuple containing

\(\theta\), array of colatitude coordinates in \([0,\pi]\)
\(\phi\), array of azimuth/longitude coordinates in \([0,2\pi]\)

orthopoly.spherical_harmonic.grid_icosahedral(nsub)#

Generates an icosahedral grid with a given number of subdivisions

Parameters:

nsub (int) – number of times to subdivide the initial 20 faces of the icosahedron. The number of cells increases rapidly with more subdivisions and is \(20(4^{\textrm{nsub}})\)

Returns:

tuple containing

\(\theta\), array of colatitude coordinates in \([0,\pi]\)
\(\phi\), array of azimuth/longitude coordinates in \([0,2\pi]\)

orthopoly.spherical_harmonic.spectrum(a, yn, ym)#

Computes the power spectrum of a spherical harmonic expansion, the total power per degree. Because the harmonics are orthonormal, each function’s coefficient is simply squared to compute its power. The squared coefficients of all orders within a degree are averaged.

Parameters:

a (array) – spherical harmonic expansion coefficients
yn (array) – the degrees of the functions in the expansion
ym (array) – the orders of the functions in the expansion

Returns:

tuple containing

array of sorted array of degrees for each power
array of power for each degree represented in yn

orthopoly.spherical_harmonic.noise(N, p, tol=1e-12, seed=1)#

Generates the coefficients for a random triangular spherical harmonic expansion with a specific relationship between the degree and the power spectral density (noise)

Parameters:

N (int) – maximum degree in expansion
p –
exponent of power spectral density relationship with degree, so that the power in each degree \(n\) is proportional to \(n^p\). The following colors, input as strings, will work
- ’red’: p = -2
- ’pink’: p = -1
- ’white’: p = 0
- ’blue’: p = 1
- ’violet’: p = 2
tol (float) – bisection method relative tolerance when normalizing across a single degree’s coefficients for the total power
seed (int) – optional seed for random number generator

Returns:

Expansion object with expansion coefficients for noise

class orthopoly.spherical_harmonic.Expansion(a, yn, ym)#

Bases: object

Stores the expansion coefficients and degree-order pairs of a spherical harmonic expansion and provides a convenient way to evaluate the expansion and its properties. To evaluate the expansion, simply call the object on arrays of spherical coordinates.

Parameters:

a (array) – coefficients of spherical harmonic expansion
yn (array) – degrees of functions in expansion
ym (array) – orders of functions in expansion

property a#: Coefficients of expansion

property yn#: Degrees of functions in expansion

property ym#: Orders of functions in expansion

property spectrum#: Power density of expansion

property unpack#: Return tuple with a, yn, ym